凸优化理论与算法

凸优化是机器学习中非常重要的一个领域，它涉及到数学、计算机科学和统计学等多个学科的知识。凸优化的目标是寻找一个凸函数的全局最小值，这个凸函数可以描述一个机器学习问题的目标函数，例如最小化损失函数或正则化函数。凸函数具有良好的性质，使得它们的最优解可以被高效地计算出来，这在机器学习中非常有用。

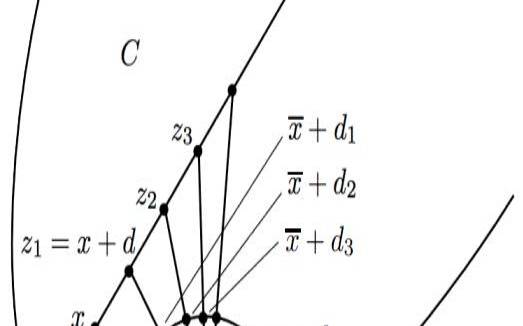
算法方面的研究则涉及到如何高效地求解凸优化问题。常见的凸优化算法包括梯度下降法、共轭梯度法、牛顿法等等。这些算法可以通过不同的方式利用凸函数的性质，使得我们可以高效地找到最优解。此外，还有一些特殊的凸优化问题，例如线性规划、二次规划等等，它们都有特定的求解算法。

凸优化在机器学习中的应用非常广泛。例如，在支持向量机中，我们需要求解一个凸二次规划问题；在逻辑回归中，我们需要最小化一个凸损失函数；在Lasso和Ridge回归中，我们需要最小化一个带有L1或L2正则化项的凸函数。这些问题都可以被视为凸优化问题，并且可以通过各种凸优化算法高效地求解。

凸优化是机器学习中非常重要的一个研究领域，它涉及到理论和算法两个方面，对于我们理解机器学习算法的性质和性能非常有帮助。在实践中，凸优化算法可以被应用于各种机器学习问题的求解中，提高算法的效率和精度。